一、概念

线性回归是一种有监督的回归分析技术,其是找出自变量与因变量之间的因果关系,本质上是一个函数估计的问题。回归分析的因变量应该是连续变量,若因变量为离散变量,则问题就转化为分类问题。回归分析主要应用场景为预测,常用的算法有如下:线性回归、二项式回归、岭回归、Lasso等。
二、模型的表达式及推导

现有如下训练集:
D={(X1,Y1),(X2,Y2),...,(Xn,Yn)}
写成矩阵形式:
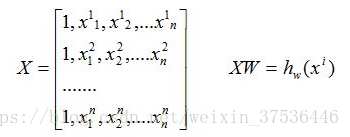
现在目的是对于给定的X找出W的最优解
采用最小二乘法来求解:先假设这个线的方程成立,然后把样本数据点代入假设的方程得到观测值,求使得实际值与观测值相减的平方和最小的参数。对变量求偏导联立便可求。
因此我们可以得到如下的损失函数:
推导:
目标是求的W使得损失函数的值最小,求解如下:
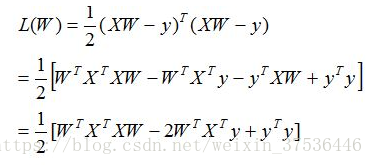
对W求偏导,得出如下结果:
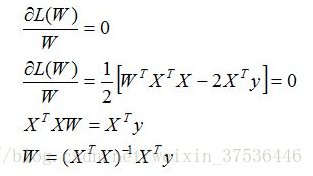
本文主要介绍线性回归的一般推导,后续会推出采用梯度下降法求上述解的过程。
代码实例
本文在实现线性回归的技术时,为了作为对比,采用了多种回归算法技术,如普通线性回归,贝叶斯回归,SVM,集成算法等,这样对于算法的选择有一个比较。下面来看具体代码实现:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt #导入图形展示库
from sklearn.linear_model import BayesianRidge,LinearRegression,ElasticNet #批量导入要实现的回归算法
from sklearn.svm import SVR #SVM中的回归算法
from sklearn.ensemble.gradient_boosting import GradientBoostingRegressor #集成算法
from sklearn.model_selection import cross_val_score #交叉检验
from sklearn.metrics import explained_variance_score,mean_absolute_error,mean_squared_error,r2_score #批量导入指标算法
raw_data=np.loadtxt('D:\\data\\regression.txt')
x=raw_data[:,:-1] #分隔自变量
y=raw_data[:,-1] #分隔因变量
#训练回归模型无锡妇科检查医院 http://www.87554006.com/
n_folds=6 #设置交叉检验的次数
model_br=BayesianRidge() #建立贝叶斯岭回归模型对象
model_lr=LinearRegression() #建立普通线性回归模型对象
model_etc=ElasticNet() #建立弹性网络回归模型
model_svr=SVR() #建立支持向量机回归模型
model_gbr=GradientBoostingRegressor() #建立梯度增强回归模型对象
model_names=['BayesianRidge','LinearRegression','ElasticNet','SVR','GBR'] #不同模型的名称列表
model_dic=[model_br,model_lr,model_etc,model_svr,model_gbr] #不同模型对象名称的列表
cv_score_list=[] #交叉验证结果列表
pre_y_list=[] #各个回归模型预测的y值列表
for model in model_dic: #读出每个回归模型对象
scores=cross_val_score(model,x,y,cv=n_folds) #将每个回归模型导入交叉检验模型中做训练检验
cv_score_list.append(scores) #将交叉验证结果存入到结果列表
pre_y_list.append(model.fit(x,y).predict(x)) #将回归训练中得到的预测y存入到列表
#模型效果指标评估
n_samples,n_features=x.shape #总样本量,总特征数
model_metrics_name=[explained_variance_score,mean_absolute_error,mean_squared_error,r2_score] #回归评估指标对象集
model_metrics_list=[] #回归评估指标列表
for i in range(5): #循环每个模型索引
tmp_list=[] #每个内循环的临时结果列表
for m in model_metrics_name: #循环每个指标对象
tmp_score=m(y,pre_y_list[i]) #计算每个回归指标结果
tmp_list.append(tmp_score) #将结果存入每个内循环的临时结果列表
model_metrics_list.append(tmp_list) #将结果存入到回归评估指标列表
df1=pd.DataFrame(cv_score_list,index=model_names) #建立交叉验证的数据框
df2=pd.DataFrame(model_metrics_list,index=model_names,columns=['ev','mae','mse','r2']) #建立回归指标的数据框
print ('samples:%d\t features:%d' % (n_samples,n_features)) #打印输出样本量和特征数量
print (90*'-') #打印分隔线
print ('cross validation result:') #打印输出标题
print (df1) #打印输出交叉检验的数据框
print (90*'-') #打印输出分隔线
print ('regression metrics:') #打印输出标题
print (df2) #打印输出回归指标的数据框
print (90*'-') #打印输出分隔线
print ('short name \t full name') #打印输出缩写和全名标题
print ('ev \t explained_variance')
print ('mae \t mean_absolute_error')
print ('mse \t mean_squared_error')
print ('r2 \t r2')
print (90*'-') #打印输出分隔线
运行结果
------------------------------------------------------------------------------------------
指标解释:
从上图中可以看出:增强梯度(GBR)回归效果是所有模型中回归效果最好的,从回归矩阵(regression metrics)中看出其方差解释ev达到了0.975,并且其平均绝对误差和均方差都是最低的,分别为1.152、2.100。从交叉验证的结果可以看出,GBR在交叉验证的6次验证中,其结果的稳定性相对较高,这证明该算法在应对不同的数据时稳定效果较好。
模型效果的可视化
模型拟合好以后,可以将几种回归效果借助matplotlib进行展示。代码如下:
#模型效果的可视化
plt.figure #创建画布
plt.plot(np.arange(x.shape[0]),y,color='k',label='true y') #画出原始值得曲线
color_list=['r','b','g','y','c'] #颜色列表
linesytle_list=['-','.','o','v','*'] #样式列表
for i,pre_y in enumerate(pre_y_list):
plt.plot(np.arange(x.shape[0]),pre_y_list[i],color_list[i],label=model_names[i]) #画出每条预测结果线
plt.title('regression result comparison') #标题
plt.legend(loc='upper right') #图例位置
plt.ylabel('real and predicted value') #y轴标题
plt.show() #展示图像
另外有需要云服务器可以了解下创新互联cdcxhl.cn,海内外云服务器15元起步,三天无理由+7*72小时售后在线,公司持有idc许可证,提供“云服务器、裸金属服务器、高防服务器、香港服务器、美国服务器、虚拟主机、免备案服务器”等云主机租用服务以及企业上云的综合解决方案,具有“安全稳定、简单易用、服务可用性高、性价比高”等特点与优势,专为企业上云打造定制,能够满足用户丰富、多元化的应用场景需求。